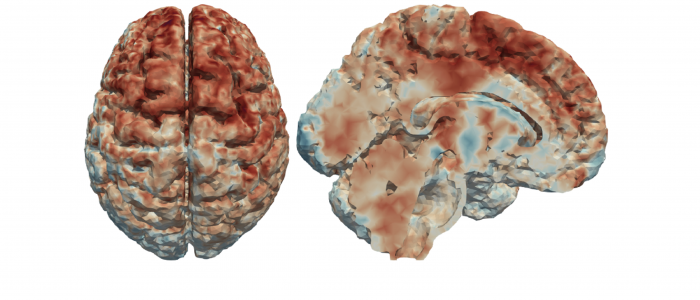
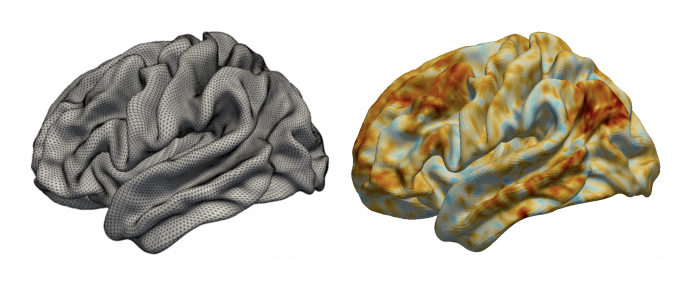
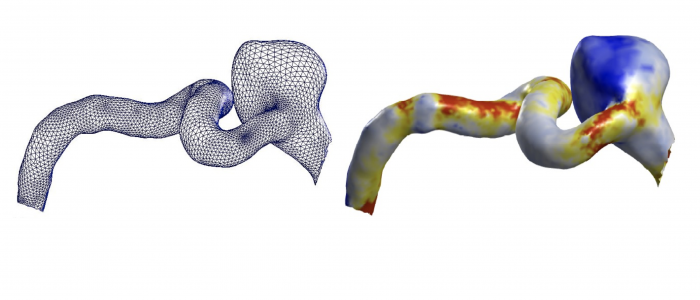
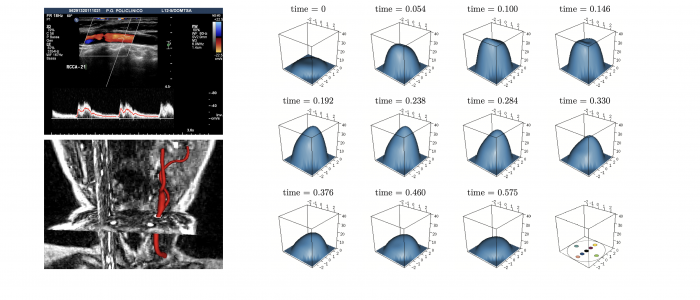
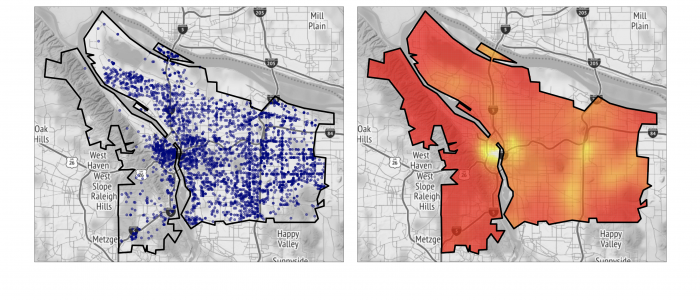
Spatial Regression with Partial Differential Equation regularization (SR-PDE) is a novel class of models for the analysis of spatially (and space-time) distributed data, that merges advanced statistical methodology and numerical analysis techniques. Thanks to the combination of potentialities from these two scientific areas, the proposed class of models has important advantages with respect to classical spatial data analysis techniques. SR-PDE is able to efficiently deal with data distributed over irregularly shaped domains, with complex boundaries, strong concavities and interior holes [1]. Moreover, it can comply with specific conditions at the boundaries of the problem domain [1, 2, 3], which is fundamental in many applications to obtain meaningful estimates. The proposed models have the capacity to incorporate problem-specific prior information about the spatial structure of the phenomenon under study, formalized in terms of a governing partial differential equation; this very flexible modeling of space-variation allows to naturally account for anisotropy and non-stationarity [2, 3, 10, 11]. Space-varying covariate information is also included in the models via a semiparametric framework. A generalized linear setting allows for response variables having any distribution within the exponential family [8], including also Poisson count data. Quantile regression is also possibile in this modeling framework, along the lines discussed in Density estimation from point-pattern data is described in [19, 20, 21]. Spatial regression with differential regularizations can also deal with data scattered over non-planar domains, specifically over Riemannian manifold domains, including surface domains with non-trivial geometries [4, 5, 6, 7, 13] and non-convex volumes [22, 23]. This has fascinating applications in the earth-sciences, in the life-sciences [4, 5, 6, 13, 22] and in engineering [7]. The models can also be extended to space-time data and spatially dependent functional data [9, 11, 12, 13, 25]. Moreover, building on these regression models, it is possible to define a principal component analysis technique for signals spatially distributed over complex domains [6, 22, 24], thus enabling population studies. The use of advanced numerical analysis techniques, and in particular of the finite element method and of isogeometric analysis [7], makes the models computationally very efficient [24]. Some first results on the consistency of the estimators are given in [18] and on inferential methods for the linear part of the models in [16, 17]. Introductions to this line of reserach are given in [14, 15]. Some computational aspects are discussed in [24]. An R/C++ library implementing these models is released via The Comprehensive R Archive Network [29].
Download code:
 fdaPDE library under development in GitHub
fdaPDE library under development in GitHub
References
- Sangalli*, L.M., Ramsay, J.O., Ramsay, T.O. (2013),
Spatial spline regression models,
Journal of the Royal Statistical Society Ser. B, Statistical Methodology, 75, 4, 681-703.
PDF Postprint Code - Azzimonti#, L., Nobile, F., Sangalli*, L.M., Secchi, P. (2014),
Mixed Finite Elements for spatial regression with PDE penalization,
SIAM/ASA Journal on Uncertainty Quantification, Vol. 2, No. 1, pp. 305-335.
PDF Postprint Code - Azzimonti#, L., Sangalli*, L.M., Secchi, P., Domanin, M., Nobile, F. (2015),
Blood flow velocity field estimation via spatial regression with PDE penalization,
Journal of the American Statistical Association, Theory and Methods, 110 (511), 1057-1071.
PDF Postprint Supplementary material Code - Dassi, F., Ettinger#, B., Perotto, S., Sangalli, L.M. (2015),
A mesh simplification strategy for a spatial regression analysis over the cortical surface of the brain,
Applied Numerical Mathematics, Vol. 90, pp. 111-131.
PDF Postprint Code - Ettinger#, B., Perotto, S., Sangalli*, L.M. (2016),
Spatial regression models over two-dimensional manifolds,
Biometrika, 103 (1), 71-88.
PDF Postprint Supplementary material Code - Lila#, E., Aston, J.A.D., Sangalli, L.M. (2016),
Smooth Principal Component Analysis over two-dimensional manifolds with an application to Neuroimaging,
Annals of Applied Statistics, 10 (4), 1854-1879.
PDF PostprintCode - Wilhelm#, M., Dede’, L., Sangalli, L.M., Wilhelm, P. (2016),
IGS: an IsoGeometric approach for Smoothing on surfaces,
Computer Methods in Applied Mechanics and Engineering, 302, 70-89.
PDF Postprint - Wilhelm#, M., Sangalli*, L.M. (2016),
Generalized Spatial Regression with Differential Regularization,
Journal of Statistical Computation and Simulation, 86 (13), 2497-2518.
PDF Postprint Code - Bernardi#, M.S., Sangalli*, L.M., Mazza#, G., Ramsay, J.O. (2017),
A penalized regression model for spatial functional data with application to the analysis of the production of waste in Venice province,
Stochastic Environmental Research and Risk Assessment, 31 (1), 23-38.
PDF Postprint Code - Bernardi#, M.S., Carey, M., Ramsay, J.O., and Sangalli*, L.M. (2018),
Modeling spatial anisotropy via regression with partial differential regularization,
Journal of Multivariate Analysis, 167, 15-30.
PDF Postprint Code - Arnone#, E., Azzimonti#, A., Nobile, F., and Sangalli*, L.M. (2019),
Modelling spatially dependent functional data via regression with differential regularization,
Journal of Multivariate Analysis, 170, 275-295.
PDF Postprint Code - Arnone#, E., Sangalli*, L.M. and Vicini, A. (2022),
Smoothing spatio-temporal data with complex missing data patterns,
Statistical Modelling, DOI: 10.1177/1471082X211057959.
PDF Postprint Code - Ponti#, L., Perotto, S. and Sangalli, L.M. (2022),
A PDE-regularized smoothing method for space-time data over manifolds with application to medical data,
International Journal for Numerical Methods in Biomedical Engineering, 38, 12, e3650.
PDF Code - Sangalli*, L.M. (2020),
A novel approach to the analysis of spatial and functional data over complex domains,
Quality Engineering, 32, 2, 181-190,
followed by discussions and a rejoinder by the author.
PDF Postprint Code
Sangalli*, L.M. (2020),
Rejoinder,
Quality Engineering, 32, 2, 197-198.
PDF - Sangalli*, L.M. (2021),
Spatial regression with partial differential equation regularization,
International Statistical Review, 89, 3, 505-531.
PDF Code - Arnone#, E., Kneip, A., Nobile, F. and Sangalli*, L.M. (2022),
Some first results on the consistency of spatial regression with partial differential equation regularization,
Statistica Sinica, 32, 209-238.
PDF Postprint - Ferraccioli#, F., Sangalli*, L.M., Finos, L. (2022),
Some first inferential tools for spatial regression with differential regularization,
Journal of Multivariate Analysis, DOI: 10.1016/j.jmva.2021.104866.
PDF Postprint - Ferraccioli#, F., Sangalli, L.M., Finos, L. (2023),
Nonparametric tests for semiparametric regression models”,
TEST, to appear. - Ferraccioli#, F., Arnone#, E., Finos, L., Ramsay, J.O., Sangalli*, L.M. (2021),
Nonparametric density estimation over complicated domains,
Journal of the Royal Statistical Society Ser. B, Statistical Methodology, 83, 346-368.
PDF Code - Arnone#, E., Ferraccioli#, F., Pigolotti#, C., Sangalli*, L.M. (2022),
A roughness penalty approach to estimate densities over two-dimensional manifolds,
Computational Statistics and Data Analysis, 174, 107527.
PDF Postprint Code - Begu#, B., Panzeri#, S., Arnone, E., Carey, M., and Sangalli*, L.M. (2024),
A nonparametric penalized likelihood approach to density estimation of space-time point patterns,
Spatial Statistics, DOI: 10.1016/j.spasta.2024.100824.
PDF Code - Arnone#, E., Negri#, L., Panzica, F. and Sangalli*, L.M. (2023),
Analyzing data in complicated 3D domains: smoothing, semiparametric regression and functional principal component analysis,
Biometrics, DOI: 10.1111/biom.13845.
PDF Code - Clementi#, L., Arnone, E., Santambrogio, M., Franceschetti, S., Panzica, F. and Sangalli*, L.M. (2023),
Anatomically compliant modes of variations: new tools for brain connectivity,
Plos One, DOI: 10.1371/journal.pone.0292450.
PDF Code - Arnone, E., De Falco, C., Formaggia, L., Meretti, G., and Sangalli, L.M. (2023),
Computationally efficient techniques for spatial regression with differential regularization,
International Journal of Computer Mathematics, DOI: 10.1080/00207160.2023.2239944.
PDF Code - Palummo#, A., Arnone, E., Formaggia, L., and Sangalli*, L.M. (2024),
Functional principal component analysis for incomplete space-time data ,
Environmental and Ecological Statistics, DOI: doi.org/10.1007/s10651-024-00598-7.
PDF Code - Castiglione#, C., Arnone, E., Bernardi, M., Farcomeni, A., and Sangalli*, L.M. (2024),
PDE-regularised spatial quantile regression,
Journal of Multivariate Analysis, DOI: 10.1016/j.jmva.2024.105381.
PDF Code - Tomasetto#, M., Arnone, E., and Sangalli*, L.M. (2024),
Modeling anisotropy and non-stationarity through physics-informed spatial regression ,
Environmetrics, DOI: 10.1002/env.2889.
PDF Code - Cavazzutti#, M., Arnone, E., Ferraccioli, F., Galimberti#, C., Finos, L., and Sangalli*, L.M. (2024),
Sign-flip inference for spatial regression with differential regularisation,
Stat, 13, 3, DOI: 10.1002/sta4.711.
PDF Code - Arnone, E., Clemente#, A., Sangalli, L.M., Lila#, E., Ramsay, J., and Formaggia, L. (2023),
fdaPDE: Physics-Informed Spatial and Functional Data Analysis, R package available from CRAN
https://cran.r-project.org/package=fdaPDE
Other publications by L.M. Sangalli